Recently, I created a set of flashcards of single Chinese characters, to practice writing. The front of my Anki cards contained the pinyin, definition, and clozes for the most common words containing the character, while the back of the card was simply the character. I tagged the cards in groups of 200 by frequency rank, using tags of “1-200”, “201-400”, etc. I already know a number of characters, so I decided to start practicing with the more infrequent characters, the “1601-1800” tag.
There were some characters I was well familiar with. Other characters took more time to remember how to write, but weren’t too difficult, as I knew the characters on sight from extensive reading. But every once in a while I would be shown a card, and it would be for a character I had never seen before in 6 years! Some like 贼 (zéi, thief) or 鹏 (péng a mythical bird) were surprising to see in the 1600-1800 range for frequency ranks, ranked more frequent in the Lancaster Corpus than 垂 (chuí to hang down) and 夹 (jiā to squeeze). But however unusual they were, I still recall encountering them at some point (金色飞贼 is the golden snitch in Quidditch from Harry Potter, and 鹏 was from reading on Chinese mythical animals). However, 琉 (liú glazed tile) and 鲍 (bào abalone) don’t look familiar at all, and I am fairly certain I have never seen the characters 萼 (è calyx of a plant) and 懋 (mào diligent) in over 6 years of study. Is it just a strange chance that I haven’t encountered them, is it failing memory, or are they more rare than their frequency would suggest?
Dispersion of Chinese Characters
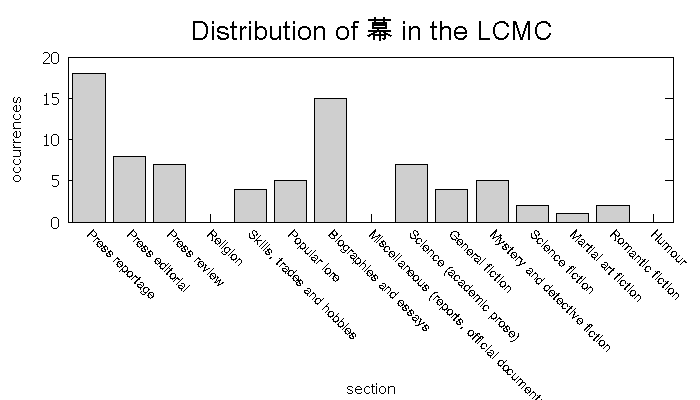
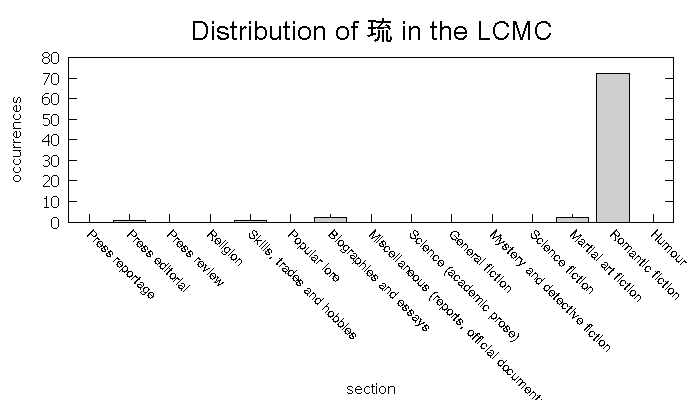
The Lancaster Corpus consists of 500 different texts, each around 3,000 characters in length. These are categorized into 15 different sections by topic–news, science, romantic fiction, etc. Here are distribution profiles for 幕 and 琉, each with a total of 78 occurrences in the corpus, and a frequency rank of 1611.
There is a significant amount of variation in the type of texts 幕 occurs in. It seems to favor non-fiction texts, although not exclusively. However, the degree of variance pales in comparison to that of 琉. Of the 78 occurrences of 琉, 72 of them are found in romantic fiction. If I drill down to the level of the individual text, I find that all 72 of these occurrences are from a single text, P17, or ” 一个女孩的浪漫故事”. In that text, 琉璃 is a person’s name. In light of that information, I would prefer not to spend study time on this character (not a pun). Note that if I exclude text P17 from my word counts, the word rank for 琉 would drop from 1615 to 3427. Ideally, there would be some kind of computational method I could apply to all characters, penalizing the ones with such skewed usage.
Dispersion in computational linguistics refers to the degree to which a word is evenly distributed in a corpus. A word with 100% dispersion would occur at equally spaced intervals. A word with 0% dispersion would be found in one contiguous group and nowhere else in the corpus. There are various ways of computing a particular word’s dispersion coefficient. In a parts-based measure, the corpus is divided up into (ideally) equal segments, and the number of occurrences of the word in each division is used for computation. In a distance-based measure, the gaps between consecutive occurrences of the word in question are measured, and a statistical function is used on these values.
To borrow an illustration from Stefan Gries1, imagine a corpus consisting of 50 letters. The corpus has been divided into n = 5 equally-sized parts.
b a m n i b e u p k | b a s a t b e w q n | b c a g a b e s t a | b a g h a b e a a t | b a h a a b e a x a
The letter a occurs once in segment 1, twice in segment 2, etc., to yield a vector of frequencies v[1..5] = (1, 2, 3, 4, 5), and a total frequency v of 15. Some simple parts-based estimates of dispersion for a would be to count the number of segments a occurs in (i.e., 5), or the maximum count – minimum count (5 – 1 = 4). Of the more complex parts-based computations, one well-known formula is from Juilland et. al, which utilizes the population standard deviation (s) of the frequency vector:
D = 1 – s/v/sqrt(n-1)
For the letter a, the value of D is 0.764. The letter b, which is distributed evenly with a vector of (2, 2, 2, 2, 2), has a frequency of 10 and a D value of 1. The letter x, which only occurs once and only in one section, has a D value of 0. Various measures of dispersion all have their own strengths and weaknesses, such as being undersensitive or oversensitive to segments with zero occurrences of the word, or having identical dispersion coefficient for different distribution profiles.
Once coefficients of dispersion are determined for words in a corpus, what do we do with this information? Our goal is to somehow adjust the raw frequencies so that poorly dispersed words are deemphasized. Juilland has proposed a simple multiplication of the two factors, dispersion and the raw frequency:
Juilland et. al. (1971): U = D * v
For the letter a in the example, this yields an adjusted frequency of 11.047, while for b it remains unchanged at 10, and for x it become 0. An adjusted frequency of zero for a word that obviously does occur may or may not be a detriment, depending on how the results are used. Besides Juilland’s formulas, there are a number of other proposed methods for calculating dispersion and adjusted frequencies. Knowing which of these is the best method is unclear at this point, and at this point is a matter of personal interpretation. Gries 2 has performed psycholinguistics experiments in which subjects are tested for word recognition times and for lexical decision times, both of which are related to word frequency. While some correlation was found, indicating that adjusting frequencies based on dispersion really can improve on the raw frequencies when representing word occurrences, the effects weren’t very large, and many different dispersion measures yielded similar effects. Juilland’s formulas were among the best. This is fortunate for me, because they are quite easy to calculate in Excel.3
Evaluating Adjusted Frequencies of Chinese Characters
Whatever the theory, what I am looking for is a method to improve my flashcard experience. I eventually suspended the Anki cards for 萼, 懋, and others after failing to learn them over 10 times in a row. What I did was take the data for all 4,721 characters in the Lancaster Corpus among the 15 sections and apply the formulas from Juilland to arrive at the adjusted frequencies. I used a modified method in which the segment counts were adjusted by a normalizing factor, because the segments were of unequal size. In this analysis I was not concerned that some of the adjusted frequencies would be zero. Many of these are cases in which there is one occurrence of the word in the entire corpus, so they are are already at the end of the rankings. I was more interested in the effects in the higher ranks (the top 2,000 or so). Below is a summary of the highlights.
| Ranks | Most penalty (rank change) | Most benefit (rank change) |
|---|---|---|
| 1-500 | 案 (-193); 球 (-172); 划 (-142); 专 (-134); 族 (-131) | 随 (56); 视 (58); 落 (59); 包 (60); 断 (64) |
| 501-1000 | 佛 (-569); 宗 (-555); 拜 (-406); 审 (-306); 爸 (-297) | 遍 (88); 遇 (91); 旧 (91); 尚 (92); 端 (95) |
| 1001-1500 | 侦 (-926); 蔬 (-824); 崇 (-777); 卦 (-776); 仲 (-712) | 恢 (143); 赞 (146); 踏 (146); 弃 (157); 享 (169) |
| 1501-2000 | 萼 (-2235); 懋 (-2227); 迦 (-2078); 琉 (-1407); 儒 (-1369) | 尝 (181); 诱 (182); 衷 (193); 屈 (199); 吞 (215) |
The characters that are the most poorly dispersed in the corpus receive the largest penalty from their raw frequency, and thus the word ranks change the most dramatically. Among the 500 most frequent characters in the Lancaster Corpus, 案 (àn legal case), suffers a large penalty because 43% of its occurrences are in the Mystery and detective fiction segment of the corpus, and 球 (qiú ball) is similarly affected with 59% of its usage in Skills, trades and hobbies. The downshifting in ranks seem to affect characters used in words for specialized domains, which is what we would expect. The only real surprise for me is that 蔬 (shū vegetable) has been adjusted so greatly, from rank 1441 to 2265. This doesn’t seem intuitive from my reading experience. However, it’s hard to argue against the corpus data in which 78% of its usage is in the Skills and trades segment.
One effect of these adjustments is that the gaps they leave shift the nearby characters to higher ranks. This affects large ranges of characters, so that the upward adjustments are not as dramatic, but the characters that benefit the most are the ones most evenly distributed. The table above summarizes the top 5 changes in each range. These characters listed are certainly useful and ubiquitous, at least for the ranks up to 1500. Regarding the positively impacted characters listed for the 1500-2000 ranges, I am not as keen on. I have certainly seen them all before on multiple occasions. But, other than 吞, I wouldn’t consider them common. However, the texts in the corpus bear out their favorable dispersion in the analysis. For a character like 衷, which I rarely see (or at least remember seeing), the character does appear in all segments of the corpus, both fiction and non-fiction. It appears in a number of different words–由衷 4, 衷心, 衷肠, 初衷, among many others–and most of these words are also well dispersed.
I have found these results useful for my study of Chinese characters using flashcards. I now have a justification for suspending cards that seem rare or overly difficult for their alleged frequency rank. The complete data is available here.
-
Gries, Stefan Th.; 2008; Dispersions and adjusted frequencies in corpora. International Journal of Corpus Linguistics 13(4). 403-437.
↩ -
Gries, Stefan Th.; 2010; Dispersions and adjusted frequencies in corpora: further explorations; Language & Computers; Vol. 71 Issue 1, p197.
↩ -
Starting from a list of characters and section, make use of Excel’s pivot table function. This will yield a table with each row having a single character and the counts for each of the 15 sections. The basic formula for D is “=1-STDEVP(B5:P5)/AVERAGE(B5:P5)/SQRT(COUNTA($B$4:$P$4)-1)”. For a more precise calculation assuming unequal section sizes, divide each character count by the total size of each section in turn.
↩ -
I don’t recall encountering this word before. But now that I have, I will no doubt be seeing it everywhere.
↩

3 Comments to 'Improving Character Frequency Lists with Dispersion Data'
February 12, 2013
Hi Chad,
you’ve posted again a superb piece of text summarizing a lot of important stuff regarding frequency and dispersion. This is written in such a clear and concise style that even people studying Mandarin who “dont care about frequencies” should be able to understand.
You’ve also found the right man, Stefan Gries. This guy is the guy to follow if you want to check on quality corpus linguistics stuff. I say quality, because nowadays a lot of people in the linguistics field seems to be doing and publishing a lot of “corpus based XYZ” study/list/analyzis etc without any basic knowledge of maths/statiscis/computing.
I would recommend also these guys (you can find them reading Gries papers)
– Stefan Evert : the main developer of the CWB CorpusWorkBench tool (Perl) ; has a lot of papers, perl scripts, Multilingual Word Expressions tools and studies
– Nick Ellis, Norbert Schmitt (and the classics Douglas Biber, John Sinclair) for everything related to collocations, lexical bundles, formulaic language ; really worth reading their papers, because you end up learning a lot about psycholinguistics and the effects of dispersion on learning
– Mark Davies ; is corpus are the base for the recent “Frequency Dictionary of …” English/Spanish/Portuguese. Read how he made the decisions on the adjusted frequencies and how he ended up using Juilland’s coefficient and balancing the registers.
The only thing you haven’t found, IMHO, is the right Corpus to spend your time and efforts with. The LCMC is too much overrated simply because it’s freely available, was done at a “respected university”, and complies with a lot of (irrelevant ) standards for corpus preparation and classification, and tagging (TEI, XML etc etc) . But the core issue for me is its just not meaningful at all. It’s too small, not balanced and not representative. It’s authors’ just spent a lot of british tax payer’s money, having people in China scanning novels, historical and more formal texts in libraries for “a variety of genres” that end up being irrelevant for the average Mandarin Learner.
I cannot recommend you the also freely available SUBTLEX-ZH subtitles corpus enough.
http://google.com?q=subtlex-ch
Take the time to read the papers associated with it. You’ll also be lead to a lot of other studies in the effects of frequency and dispersion in language learning
February 12, 2013
Check out the introduction of Mark Davies “Frequency Dictionary of Spanish”. Cannot recommend you enough.
google,
“ishare 英语原版语言学及小语种学习书籍 Davies.-.A.Frequency.Dictionary.of.Spanish”
and for the Englsh one,
http://www.wordfrequency.info/files/book.pdf
February 12, 2013
Thanks for the comment and information! I have seen the SUBTLEX corpora (which also exists for other languages) come up in a few different searches lately. I will give it a try. I would love to have access to the Leeds corpus texts (280 million words), but prof. Sharoff has been reluctant to release them.
One advantage of the LCMC is that it has been segmented into words by hand, so it’s (presumed) more accurate than any machine-based segmenter. The biggest disadvantage I see is that the texts are dated, especially in news and press sections. 苏联 (Soviet Union) is among the top 1,000 words in the corpus, for example.